Fouriertransformation
Ganz ohne komplexe Zahlen

Eine detaillierte Erklärung mit mathematischen Beweisen

von Felix Ludwig (me@ludf.de)

Angenommen wir haben ein Signal, welches ausschließlich aus der Überlagerung von zeit-verschobenen Sinuswellen (Teilsignale) besteht. Jedes Teilsignal muss periodisch sein, sodass das Gesamtsignal dies ebenfalls ist. Im diskreten Fall werden wir ausschließlich Signale mit einer maximalen Frequenz von \( \frac{n}{2} \) betrachten, wobei n die die Anzahl der Datenpunkte pro Sekunde ist (Samplerate).

Betrachtet man den kleinsten Zeitraum, in dem alle Teilsignale mindestens eine Periode und genau ein ganzes Vielfaches ihrer Periode vervollständigt haben, so erhält man beispielsweise den nachfolgenden Plot.

Die Summe der Signale entsteht durch die Addition der Teilsignale. Nachfolgend beschäftigen wir uns mit der Aufgabe aus dem Gesamtsignal die Teilsignale ausfindig zu machen.

Das Konzept basiert darauf, dass wir das Gesamtsignal immer wieder darauf überprüfen, ob ein Teilsignal in ihm vorhanden ist. Also testen wir für jedes Teilsignal mit spezifischer Periodizität (Frequenz), ob das Teilsignal im Gesamtsignal vorhanden ist. Die Rückgabe dieses Algorithmus ist eine Liste an Magnituden. Jede Magnitude repräsentiert die Magnitude zum zugehörigen Teilsignal.

Betrachten wir nun eine grobe Skizze dieses eben genannten Algorithmus: 

extrahiereFrequenzen(signal):
  for minimumFrequenz ≤ frequenz ≤ maximumFrequenz:
    magnitudesfrequenz = testeAufFrequenz(signal, frequenz)
  end
  return magnitudes
endFunction

Anschließend verbleibt nun also die Aufgabe zu einem Signal und einer Frequenz die Magnitude der Frequenz zu bestimmen. Ein Teil der Arbeit übernimmt hierbei das Skalarprodukt angewandt auf zwei Signale bzw. Funktionen.

Betrachten wir nun also das Skalarprodukt zweier Funktionen. Genauer sollen beide Funktionen im Anschließenden Sinus- bzw. Kosinusfunktionen ohne (Phasen-)Verschiebung sein. Also in der Form \(s(x) = sin(x)\) oder \(s(x) = 5 \cdot sin(2 \, x)\) usw., sodass für alle \(f_i \in \mathbb{Z}_0\) und \( m_i \in \mathbb{R}\) gilt \(s_i(x) = m_i \cdot sin(f_i \cdot x)\). Das Skalarprodukt sieht dann folgendermaßen aus: \[ \left< s_i, s_j \right> = \int_0^{2 \pi} s_i(x) \cdot s_j(x) \, dx \] Nachfolgend wird gezeigt, dass folgende Eigenschaften gelten:

  1. Wenn \(f_i \ne f_j\), dann gilt \( \left< s_i, s_j \right> = 0\)
  2. Wenn \(f_i = f_j\), dann gilt \( \left< s_i, s_j \right> = m_i \cdot m_j \cdot \pi \)
Dies ist wichtig, da wir, wie oben im Algorithmus gezeigt, unser Signal immer auf eine bestimmte Frequenz "testen". Wir verlangen, dass alle anderen Frequenzen bei der Magnitudenbestimmung keinen Einfluss haben. Nur so ist eine nach Frequenz differenzierte Aussage über das Signal treffbar.

Die Bestimmung der Stammfunktion mit \(f_i \ne f_j\). \[ \begin{align*} & \int s_i(x) \cdot s_j(x) \, dx \\ &= \int m_i sin(f_i \, x) \, m_j sin(f_j \, x) \, dx \\ &= \frac{m_i m_j}{2} \int cos(x \, (f_i - f_j)) - cos(x \, (f_i + f_j)) \, dx && (sin(\alpha \, x) \, sin(\beta \, x) = cos(x \, (\alpha - \beta)) - cos(x \, (\alpha + \beta))) \\ &= \frac{m_i m_j}{2} \left( \int cos(x \, (f_i - f_j)) \, dx - \int cos(x \, (f_i + f_j)) \, dx \right) \\ &= \frac{m_i m_j}{2} \left( \frac{\int cos(u_1) \, du_1}{du_1} - \frac{\int cos(u_2) \, du_2}{du_2} \right) && (f_i \ne f_j, u_1 = x \, (f_i - f_j), \, u_2 = x \, (f_i + f_j), \\& && du_1 = f_i - f_j, \, du_2 = f_i + f_j) \\ &= \frac{m_i m_j}{2} \left( \frac{sin(x \, (f_i - f_j))}{f_i - f_j} - \frac{sin(x \, (f_i + f_j))}{f_i + f_j} \right) \end{align*} \] Das bestimmte Integral für \(f_i \ne f_j\). \[ \begin{align*} & \left< s_i, s_j \right> \\ &= \left( \frac{m_i m_j}{2} \left( \frac{sin(2\,\pi \, (f_i - f_j))}{f_i - f_j} - \frac{sin(2\,\pi \, (f_i + f_j))}{f_i + f_j} \right) \right) \\ &- \left(\frac{m_i m_j}{2} \left( \frac{sin(0 \, (f_i - f_j))}{f_i - f_j} - \frac{sin(0 \, (f_i + f_j))}{f_i + f_j} \right) \right) \\ &= \frac{m_i m_j}{2} \left(\frac{sin(2\,\pi \, (f_i - f_j))}{f_i - f_j} - \frac{sin(2\,\pi \, (f_i + f_j))}{f_i + f_j} \right) - \left( \frac{0}{f_i - f_j} - \frac{0}{f_i + f_j} \right)\\ &= \frac{m_i m_j}{2} \left(\frac{sin(2\,\pi \, (f_i - f_j))}{f_i - f_j} - \frac{sin(2\,\pi \, (f_i + f_j))}{f_i + f_j} \right) && (\text{da} \quad (f_i - f_j),(f_i + f_j) \in \mathbb{Z} \\& && \text{und} \\& &&\forall n \in \mathbb{Z}. sin(2 \, \pi \, n) = sin(0) = 0) \\ &= \frac{m_i m_j}{2} \left(\frac{0}{f_i - f_j} - \frac{0}{f_i + f_j} \right) \\ &= 0 \end{align*} \]

Die Bestimmung der Stammfunktion mit \(f_i = f_j\). \[ \begin{align*} & \int m_i sin(f_i \, x) \, m_j sin(f_j \, x) \, dx \\ &= \frac{m_i m_j}{2} \int cos(x \, (f_i - f_j)) - cos(x \, (f_i + f_j)) \, dx && (sin(\alpha \, x) \, sin(\beta \, x) = cos(x \, (\alpha - \beta)) - cos(x \, (\alpha + \beta))) \\ &= \frac{m_i m_j}{2} \left( \int cos(x \, (f_i - f_j)) \, dx - \int cos(x \, (f_i + f_j)) \, dx \right) \\ &= \frac{m_i m_j}{2} \left( \int cos(0) \, dx - \int cos(x \, 2 \, f) \, dx \right) && (f = f_i = f_j) \\ &= \frac{m_i m_j}{2} \left( x - \frac{\int cos(u) \, du}{du} \right) && (u = x \, 2 \, f, du = 2 \, f) \\ &= \frac{m_i m_j}{2} \left( x - \frac{sin(x \, 2 \, f)}{2 \, f} \right) \end{align*} \] Das bestimmte Integral mit \(f_i = f_j = f\). \[ \begin{align*} & \left< s_i, s_j \right> \\ &= \left(\frac{m_i m_j}{2} \left(2 \, \pi - \frac{sin(2 \, \pi \, 2 \, f)}{2 \, f} \right) \right) - \left(\frac{m_i m_j}{2} \left( 0 - \frac{sin(0 \, 2 \, f)}{2 \, f} \right) \right) \\ &= \frac{m_i m_j}{2} \left(2 \, \pi - \frac{0}{2 \, f} \right) \\ &= m_i \cdot m_j \cdot \pi \end{align*} \]

Mit den oben genannten und nun bewiesenen Eigenschaften lässt sich ein erster Algorithmus für unsere testeAufFrequenz-Methode angeben: 

testeAufFrequenz(signal, frequenz):
  testFunktion(x) = 1 * sin(x * frequenz)
  sklr = skalarprodukt(signal, testFunktion)
  return  sklr / (1 * PI)
endFunction

Da unsere testFunktion eine Magnitude von 1 hat, ist das Ergebnis des Skalarprodukts \( m_i \cdot 1 \cdot \pi \), weshlab in der return-Zeile durch \( 1 \cdot \pi \) geteilt wird.

Wenn unsere Aufgabe nur daraus bestände die Magnituden der \(s_i\) Funktionen zu bestimmen, wären wir hier fertig. Allerdings ist unser Signal komplexer. Unsere Teilsignale sind Phasenverschobene Sinusfunktionen. Modelieren wir diese Teilsignale also folgendermaßen: \( \mathbb{s}_i(x) = m_i \cdot sin(f_i \cdot x + \phi_i) \). Mit \( -\frac{\pi}{2} < \phi_i \leq \frac{\pi}{2} \) und \( -1 \leq m_i \leq 1 \). \( \phi \) ist bewusstermaßen ungleich \( - \frac{\pi}{2} \), da sonst eine uneindeudigkeit mit \( \phi_i = \frac{\pi}{2}, m_i = 1, \mathbb{s}_i(x) = \mathbb{s}_i(x), \phi_i = -\frac{\pi}{2}, m_i=-1 \). Leider wird es nun etwas komplexer. Die Berechnungen von oben lassen sich nicht einfach mit diesen neuen Funktionen durchführen. Die Phasenverschiebung ist das Problem. Als Lösung dessen kommt das harmonische Additionstheorem zur Hilfe. Es besagt, dass wir jedes Phasenverschobene Sinussignal als Addition von Sinus- und Cosinuswellen ohne Phasenverschiebung darstellen können. Also \( \mathbb{s}_i(x) = m_i \cdot sin(f_i \cdot x + \phi_i) = a \cdot cos(f_i \, x) + b \cdot sin(f_i \, x) \). Die beiden Magnituden a und b können wir mittels des oben vorgestellten Algorithmus bestimmen. Aus ihnen kann dann \(m_i\) berechnet werden. Nachfolgend wird der Beweis des Harmonischen Additionstheorems durchgeführt.

Harmonisches Additionstheorem: \[ \begin{align*} a \, cos(\Theta) + b \, sin(\Theta) &= c \, sin(\Theta + \phi) \\ \Leftrightarrow a \, cos(\Theta) + b \, sin(\Theta) &= c \, sin(\Theta) \, cos(\phi) + c \, cos(\Theta) \, sin(\phi) && (\text{mittels} \quad sin(\alpha + \beta) = sin(\alpha) \, cos(\beta) + cos(\alpha) \, sin(\beta)) \\ \Leftrightarrow a &= c \, sin(\phi) \wedge b = c \, cos(\phi) \\ \\ \text{Fall 1:} \, c &= 0 \\ & \Rightarrow a = 0 \wedge b = 0 \\ & \text{Die Phasenverschiebung ist} \\ & \text{hierbei nicht bestimmbar, aber auch irrelevant, da} \\ & s(x) = 0 \\ \\ \text{Fall 2:} \, c &\ne 0 \\ \text{Fall 2.1:} \, b &= 0 \\ & \Leftrightarrow cos(\phi) = 0 \Leftrightarrow \phi = \frac{\pi}{2} \\ \\ \text{Fall 2.2:} \, b &\ne 0 \Leftrightarrow \phi \ne \frac{\pi}{2} \\ \phi &= arctan(tan(\phi)) && \left(\text{für} \quad -\frac{\pi}{2} < \phi < \frac{\pi}{2} \right) \\ &= arctan \left( \frac{sin(\phi)}{cos(\phi)} \right) && \left(\text{mit} \quad tan(\alpha) = \frac{sin(\alpha)}{cos(\alpha)} \right) \\ &= arctan \left(\frac{ c \, sin(\phi)}{c \, cos(\phi)} \right) \\ &= arctan \left(\frac{a}{b} \right) \\ \\ \text{Dieses Konzept} & \text{ fassen wir in der folgenden Funktion zusammen} \\ arctan2(a, b) &= \begin{cases} undefined & ,c = 0 \Leftrightarrow a = 0 \wedge b = 0 \\ \frac{\pi}{2} & ,b = 0 \\ arctan(\frac{a}{b}) & ,b \ne 0 \\ \end{cases} \\ \\ \text{Fall 1:} \, b &= 0 \\ & \Leftrightarrow \phi = \frac{\pi}{2} \\ & \Rightarrow a = c \, sin(\frac{\pi}{2}) = c \cdot 1 \\ \text{Fall 2:} \, b &\ne 0 \\ a^2 + b^2 &= c^2 \, sin^2(\phi) + c^2 \, cos^2(\phi) \\ &= c^2 \, (sin^2(\phi) + cos^2(\phi)) \\ &= c^2 && \left( \text{da} \quad sin^2(\alpha) + cos^2(\alpha) = 1 \right) \\ \Rightarrow c &= \pm \sqrt{a^2 + b^2} \\ &= sgn(b) \, \sqrt{a^2 + b^2} && \left( \text{da für} \quad - \frac{\pi}{2} < \phi < \frac{\pi}{2} \quad cos(\alpha) > 0 \quad \text{und} \quad b \ne 0 \right) \\ \\ \text{Dieses Konzept} & \text{ fassen wir in der folgenden Funktion zusammen} \\ mag(a, b) &= \begin{cases} a & ,b = 0 \\ sgn(b) \, \sqrt{a^2 + b^2} & ,b \ne 0 \\ \end{cases} \\ \\ \end{align*} \]

Mit dem Additionstheorem ausgestattet können wir \(m_i\) berechnen. \[ m_i = \begin{cases} a & ,b = 0 \\ sgn(b) \, \sqrt{a^2 + b^2} & ,b \ne 0 \\ \end{cases} = \begin{cases} a & ,\left< sin, \mathbb{s}_i \right>/\pi = 0 \\ sgn(\left< sin, \mathbb{s}_i \right>/\pi) \, \sqrt{(\left< cos, \mathbb{s}_i \right>/\pi)^2 + (\left< sin, \mathbb{s}_i \right>/\pi)^2} & ,\left< sin, \mathbb{s}_i \right>/\pi \ne 0 \\ \end{cases} \]. Anschließend wird der verfeinerte Algorithmus für Eingangssignale mit Phasenverschiebung dargestellt. 

testeAufFrequenz(signal, frequenz):
  sinTest(x) = 1 * sin(x * frequenz)
  cosTest(x) = 1 * cos(x * frequenz)
  sinSklr = skalarprodukt(signal, sinTest)
  cosSklr = skalarprodukt(signal, cosTest)
  b = sinSklr / (1 * PI)
  a = cosSklr / (1 * PI)

  if b = 0:
    magnitude = a
  else:
    magnitude = vorzeichen(b) * quadratwurzel(quadriert(a) + quadriert(b))
  return magnitude
endFunction

Anschließend betrachten wir die Realweltanwendung der Fouriertransformation. Wir erhalten nun kein zeitindiskretes Signal, sondern ein zeitdiskretes Signal. Das bedeutet, dass unser Signal aus einer Folge von einzelnen Abtastwerten (eng. Samples) besteht. Ein solches Signal hat üblicherweise eine Abtastrate (eng. Samplerate), welche beschreibt, wie viele Samples pro Sekunde abgespielt werden sollen, um einen Ton zu erzeugen. Üblicherweise arbeiten Audiodateien mit \(44,100\) Samples pro Sekunde. Das bedeutet, dass die 1Hz Frequenz genau eine Periode in \(44,100\) Samples durchläuft. Die schnellste Frequenz bestimmt sich durch das sog. Abstasttheorem mit \(44,100 / 2 = 22,050\) Hz. In unseren zeitindiskreten Berechnungen haben wir immer einen Zeitausschnitt von 0 bis \(2\pi\) betrachtet. Analog dazu betrachten wir nun den Zeitausschnitt von 0 bis \(44,100\) Samples (oder genauer: Was immer die Abtastrate ist). Die Magnituden \(m_i\) der Phasenunverschobenen Sinusfrequenzen wurden vorher durch \(\left< sin, s_i \right> / \pi \) berechnet. Nun arbeiten wir allerdings mit der Summe von 0 bis \(44,100\), weshalb wir durch \(22,050\) teilen müssen, also \(m = \left< sin, s_i \right> / 22,050 \).

Anschließend setzen wir die Algorithmen von vorher in Python um. 

from scipy.io import wavfile
import matplotlib.pyplot as plt, mpld3
import math
import numpy as np

def skalarprodukt(signal1, signal2):
    # requires both signals to have length = samplerate.
    result = 0
    for i in range(samplerate):
        result = result + signal1[i] * signal2[i]
    return result

def vorzeichen(number):
    if number == 0:
        return None # undefined
    elif number < 0:
        return -1
    else:
        return 1

def generate_signal(function):
    # generates `samplerate` amount of samples of the
    # given function in the interval between 0 and 2pi
    signal = []
    for i in range(samplerate):
        ratio = i / samplerate # [0,1)
        uprange = ratio * 2 * math.pi # [0, 2pi)
        signal.append(function(uprange))
    return signal

def testeAufFrequenz(signal, frequenz):
    sinTest = lambda x: 1 * math.sin(x * frequenz) # for b
    cosTest = lambda x: 1 * math.cos(x * frequenz) # for a
    sinSignal = generate_signal(sinTest)
    cosSignal = generate_signal(cosTest)
    sinSklr = skalarprodukt(signal, sinSignal)
    cosSklr = skalarprodukt(signal, cosSignal)
    b = sinSklr / (1 * samplerate // 2)
    a = cosSklr / (1 * samplerate // 2)

    if b == 0:
        magnitude = a
        if a == 0:
            phase = None # undefined value
        else:
            phase = math.pi / 2
    else:
        magnitude = vorzeichen(b) * math.sqrt(a**2 + b**2)
        phase = math.atan(a / b)
    return magnitude, phase

def extrahiereFrequenzen(signal):
    magnitudes = []
    phases = []
    for frequenz in range(0, samplerate // 2 + 1): # + 1 to include end
        m, p = testeAufFrequenz(signal, frequenz)
        print(frequenz, m, p)
        magnitudes.append(m)
        phases.append(p)
    return magnitudes, phases

samplerate, data = wavfile.read('sinc.wav')

if data.dtype == np.float32 or data.dtype == np.float64:
    pass
elif data.dtype == np.int16:
    data = data / np.iinfo(np.int16).max
else:
    print(data.dtype)
    print("Wrong datatype. Abort!")
    exit(1)

magnitudes, phases = extrahiereFrequenzen(data)

plt.plot(magnitudes, '-k')
plt.title('Fouriertransformation')
plt.xlabel('Frequenz')
plt.ylabel('Magnitude')

mpld3.show()


# regenerate original signal
s = np.zeros(samplerate, dtype=np.float64)
for i in range(len(magnitudes)):
    sig = generate_signal(lambda x: magnitudes[i] * math.sin(i * x + phases[i]))
    for j in range(len(s)):
        s[j] += sig[j]

wavfile.write("retrans.wav", samplerate, s)
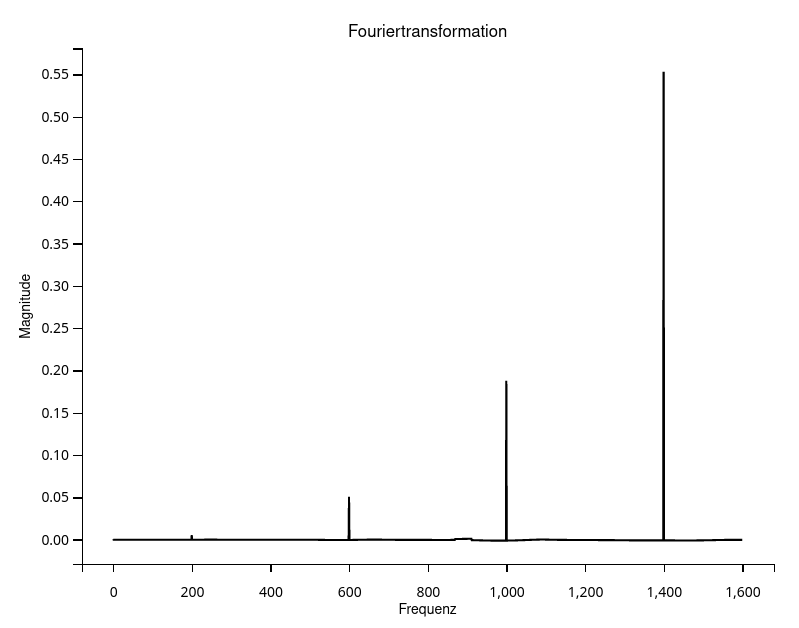
Nachfolgend sehen wir erstmals die Fouriertransformation eines Signals - angegeben ist die Magnitude (y-Achse) der Frequenzen (x-Achse) des Ausgangssignals.

Das obige Python-Programm berechnet ebenfalls die Rücktransformation als retrans.wav. Wer möchte, kann dieses Signal invertieren und auf das Ausgangssignal addieren, um ein perfektes 0-Signal zu erhalten, was die Korrektheit des Algorithmus beweist.